수학은 정말 쉽고 간단할까?
수학 공식이 적혀 있는 책은 일단 딱딱하다는 느낌이 듭니다. 수학 자체가 논리성, 간결성, 객관성을 숙명처럼 가집니다. 그렇다 보니 원칙이라는 틀이 있는 것 처럼 보입니다. 딱딱하고 재미없다는 이유 때문에 수학을 포기하는 사람이 많습니다.
과학 기술의 경우 교양 수준으로 눈높이를 낮춘 서적이 많이 나오고 있습니다. 수학자들도 과학자 못지 않게 수학을 쉽게 설명하기 위해 노력합니다. 다만, 과학보다는 아직 대중의 눈높이에 맞는 설명이 부족한 것 같습니다. 받아들이는 입장에서도 수학 자체가 재미없다는 선입견이 우선 작용하기 때문이기도 할 것입니다. 대부분의 책이 기승전’공식’이라는 틀을 벗어나지 않는 것도 부담이 됩니다.
공식을 외우기 보다는 수학적 사고가 중요하다고 합니다. 문제 풀이에서 정답보다는 그 과정이 중요하다고 합니다. 빠르게 계산할 수 있는 방법보다는 그 계산 원리가 중요하다고 합니다. 수학이라는 학문 자체는 기초 과목이지만 수학적 사고는 새로운 기술의 본질이 됩니다. 4차 산업혁명 시대, AI같은 첨단 기술이 많이 등장합니다. 이러한 기술을 이해하기 위해서라도 수학에 대한 생각을 분명 달리 해야 할 것입니다.

수학책을 탈출한 미적분 일상 생활 속 숨은 미적분 찾기
류치 저/이지수 역 | 동아엠앤비 | 2020년 07월 01일
학교 다닐때 성적만을 높이기 위해 배웠던 수학입니다. 지식으로서의 수학을 잊고 지낸지 오래 되었습니다. 하지만, 지금 수학을 다시 배우기 위해 애쓰고 있습니다. 사칙연산을 아는 것 만으로도 불편없이 살아왔는데 말입니다. 마흔살이 넘어서 수학책을 다시 보고 있습니다. 시작은 전문서적 보다는 교양 수학으로 시작합니다.
이 책을 읽고 나면 수학이 매일 밥을 먹는 것과 다르지 않다고 생각할 것이다. 아주 오래전에 어떤 음식을 먹었는지는 기억나지 않지만 그때 먹은 그 음식은 우리 몸에 영양소를 공급해 주었다. 수학을 공부하는 것도 마찬가지다. 어떤 공식을 배워도 금세 까먹을지 모르지만 그 공식을 배우고 이해하는 과정 자체가 영혼의 일부분이 된다.13쪽
이 책은 수학 공식을 설명하는 책이 아닙니다. 수학적 사고를 통해 그 공식이 나오게 된 이유를 알려줍니다. 일상에서 흔히 일어날 수 있는 일들을 예로 듭니다. 그 예를 통해 미적분이 무엇인지, 공부는 어떻게 하고, 문제를 제대로 푸는 방법을 설명합니다.
그렇다고 해도 이 책도 다른 수학책처럼 수많은 공식이 없는 것은 아닙니다. 다만 읽는 사람의 흐름을 방해하지 않는 수준으로 이야기를 풀어내고 있습니다. 복잡한 증명 과정은 없습니다. ‘왜?’라는 질문을 통해 궁금하게 만드는 것도 쉽게 읽히게 하는 하나의 방법인 것 같습니다.
첵애서는 총 10개의 사례를 소개합니다. 그 사례가 모두 수학적 사고와 연결이 됩니다. 그 수준은 고등 수학의 전반적인 지식입니다. 고등 수학에서 가장 중요시 되는 개념이 바로 미분과 적분입니다. 일단, 미분과 적분이라는 것 자체가 익숙한 개념은 아니다 보니 이 책이 꼭 쉬운 것 만은 또 아닙니다.
어떤 순간의 순간 속도는 거리의 도함수라고 배운 것처럼, 순간 속도를 미분하면 가속도를 구할 수 있다.95쪽
사례를 통해 개념을 이해했다면, 그 이해 수준을 심화학습으로 다시 질문을 합니다. 중간중간 수학에 기여한 중요 인물들도 소개하고 있습니다.
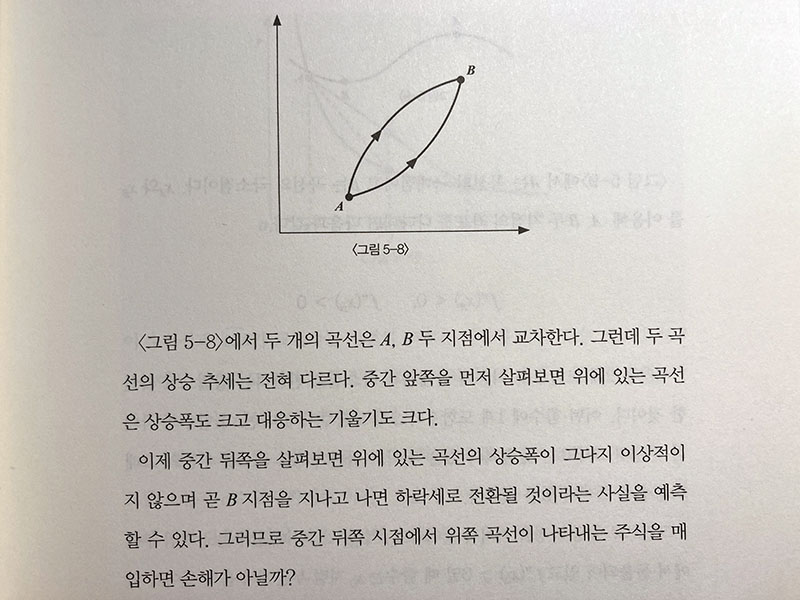
1계 도함수를 구한 다음 2계 도함수를 구하고 해당 지점에서 2계 도함수가 0보다 큰지 작은지만 확인하면 된다. 다시 말해 해당 지점에서 극대인지 극소인지를 보면 된다. 해당 지점이 극댓값이라면 주가가 곧 하락할것이므로 서둘러 매도해야 한다.122쪽
저자가 류치라는 중국사람 입니다. 그래픽 디자이너이자 해커이며, 수학의 달인으로 소개되고 있습니다. 컴퓨터 관련 프로그램을 하는 사람으로도 나옵니다. 이러한 경험을 수학에 접목하여 많은 서적을 집필하고 있다고 합니다. 우리나라 사람 및 일본사람이 지은 수학 책보다는 조금은 색다르다는 인식을 가지게 됩니다.
프로그래머 입장에서 수학은 두 부분으로 나뉜다고 합니다. 첫 번째는 수학적 사고와 같이 공식을 유도하는 과정에서 배우는 것들입니다. 두 번째는 유도된 결과로 얻어진 수식을 응용하는 것입니다. 두 번째가 바로 알고리즘입니다. 프로그래머는 알고리즘을 활용하여 프로그램을 짜고 시스템을 개발합니다. 하지만, 구축된 시스템의 근본적인 개선을 위해서는 알고리즘의 개선이 필요합니다. 쓸데없이 복잡하게 만들지 말고 간단하게 만들 수 있는 방법을 생각해야 합니다. 이것이 다시 첫 번째 과정을 고려해야 하는 이유입니다. 즉, 결국 수학의 모든 부분을 이해해야 하는 것입니다. 데이터 과학자도 마찬가지 입니다. 수학과 땔 수 없는 업무를 하는 사람입니다.
미분방정식 모형 자체가 변화하는 사물이나 현상을 간소화시켜 만든 모형이다.211쪽
수학은 쉽고 간단하다고 합니다. 이말을 믿지 못하는 이유가 우리의 생활 자체가 얼마나 복잡한지를 경험하지 못했기 때문이라고 합니다. 수학이라는 것 자체가 이런 복잡한 우리의 생활을 간단하게 설명하기 위한 것이기 때문에 쉽다는 것으로 들립니다. 이 말을 정말 믿어야 할지, 믿지 말아야 할지는 수학을 다시 배우면서 검증해야 할 것 같습니다.